Unit 1 Lab 3 Modern Art With Poygons Snap

Lab iii: Modern Fine art with Polygons

Mary still needs to review/revise this page. --MF, 5/26/20

There is a lot of todo and commented out text on this page. To be cleaned upwardly next year. --MF, 12/19/17

Brian, can we cut the text at the lesser later the standards? --MF, xi/xv/xix

the TG has to brand the plan more explicit: Paul's brilliant invention of pinwheel was to become around the whole exterior-angle problem by making the turning angle visible on the stage. Once kids understand the turning angle, /then/ you lot draw polygons as a limiting case of pinwheels. [Teachers should not, merely may exist inclined to, adapt by] starting with polygons and /then/ doing pinwheels. [This] totally misses the signal of pinwheels. --MF, 1/8/xix (Adaptation of BH email)

The post-obit HTML needs cleanup (Mary), and Brian, the images demand alt/title tags. --MF, 11/15/19

In this lab, students use a sprite not as a character in an animation, simply to depict pictures on the phase, using turtle graphics. They also have the opportunity to mimic the work of famous artists.

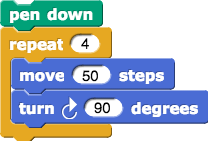
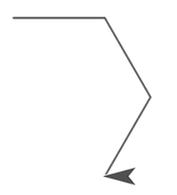
• Squares are easy, because right angles are familiar, and because the turning angle is equal to the interior angle. Merely that'southward not the case for other regular polygons. Many students' kickoff attempt (page 1) will expect like this:
  
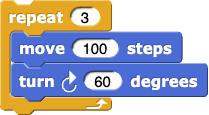
  To assist them, nosotros start with an easier problem (page two): Find the turning angle for asterisks with different numbers of spokes:
  
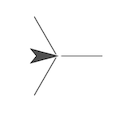
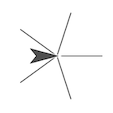
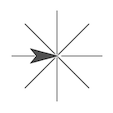
  Hither it'due south obvious that the total turning angle is 360°, that the angles between spokes are equal (in each asterisk), and that therefore each plough must exist 360°/n, where n is the number of spokes.
  But it'due south non obvious how this is connected with the polygon problem. To help, we innovate an intermediate shape, the pinwheel:
  
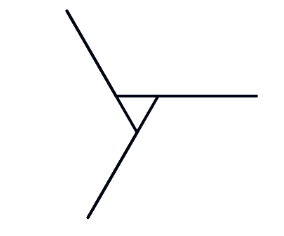
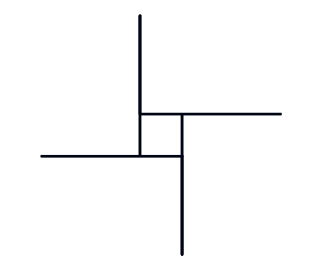
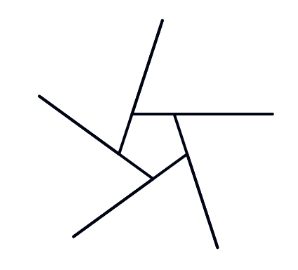
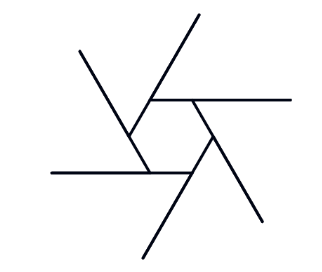
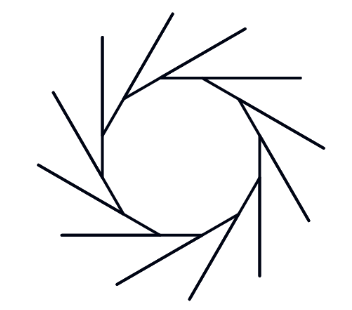
  Just as in the asterisk, each spoke of the pinwheel is fabricated by moving forward and and so backward. But what's new in the pinwheel is that the backward motion is smaller than the frontward motion, so the adjacent spoke starts partway up the previous spoke. The of import pedagogic bespeak is that the turning bending is withal visible in the picture:
  
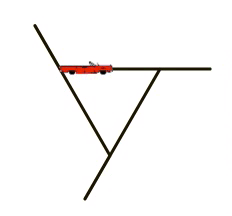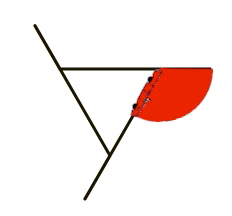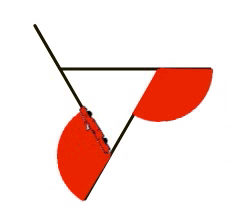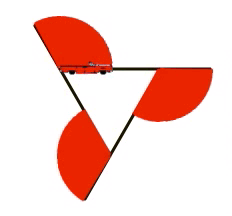
  Students then draw polygons as the limiting case of a pinwheel in which the backward motion is zero steps.
  At the same time, they are learning how to write and utilize their own procedures with inputs. This is another footstep in their understanding of abstraction: In Lab 2 they captured a repeated action past giving it a name, and in this lab they learn that they can generalize a script by making it a custom block with inputs, so that information technology can practise something a chip unlike each fourth dimension it's used.
• This lab includes Have It Further activities in which students can mimic the piece of work of various artists based on polygons:
  

  	Josef Albers	Vassily Kandinsky	Kazimir Malevich	Alma Thomas
  original
  BJC

  
  Don't assign these activities; they're all time-consuming, open-ended, and not scaffolded. Just they're a way for interested students to go by doing finger exercises considering we told them to; brand sure students notice them, and support those students who cull them, e.m., by arranging computer time for them outside of regular class meetings.

Pacing:

Lab Pages

• Page 1: Exploring Motion.
  • Learning Goals:
    • Utilize the echo block to carry out the aforementioned action several times.
    • Control the relative sprite movement with the motion block.
    • Control the relative sprite direction with the plow block.
    • Set the pen thickness with the set pen size block.
  • To launch this lab—Make a Prediction: Echo, Move, Plough
    • Project the script and inquire students to predict what it does (hash out in small groups and/or equally a class).
    • Discussion: Enquire students "How exercise programs implement algorithms?" Listen for students to recognize that programs execute instructions in social club (sequentially) and procedure each next step automatically.
  • Tips:
    • The first page of this lab gives students a simple script to draw a foursquare and asks them to experiment with it, changing various numbers in the script and observing the results. Students who are accustomed to beingness told exactly what to do may flounder. Tell them that inventiveness is ane of the Big Ideas of Computer Science Principles and that in this sort of exploratory lesson there are no wrong answers.
• Page two: Angles and Turning.
  • Learning Goals:
    • Explore the concept of turning angle through experimentation.
    • Adapt simple scripts by changing the inputs.
    • Work with multiple constraints to achieve a desired outcome.
  • Tips:
    • This page is a prelude for the upcoming pages and is an opportunity for students to experiment and brand discoveries on their own.
    • A recent update to Chrome introduced a bug that affects the Snap! set pen color to cake with the square picture of the actual color (not the block with a colour number). This is fixed in Chrome version 78.
• Page three: Blocks with Inputs.

  Brian, is this commented code still needed? If non, could you delight remove it? --MF, 11/15/xix

  • Learning Goals:
    • Learn how to generalize the functionality of a cake by introducing input parameters.
    • Gain some initial familiarity with the concept of brainchild equally a large idea in Informatics.
  • Tips:
    • This page is one of students' primeval encounters with the concept of brainchild in Computer Scientific discipline. Giving an input parameter to a cake generalizes its functionality, enabling it to reach a wider variety of tasks. Unless, this kickoff come across with brainchild is highlighted, almost students may miss what a big deal information technology is.
    • As a foreshadowing to the upcoming pages, ask students to anticipate how they tin further generalize the pinwheel block past introducing more input parameters.
    • About students may not yet exist quite set to explore creative applications of the pinwheel block every bit shown in the Have Information technology Farther. These are intended as idea-provoking ideas that they can come back to later on in the Unit.
    • At the end of class, ask students how they drew 2 pinwheels on the stage. After a few suggestions, ask students to place the most constructive strategy, guiding them to conclude that using the pinwheel block twice is better than other options (e.grand., copying and pasting the aforementioned lawmaking, creating a second block called second pinwheel).
• Folio iv: Change Your Pinwheel.
  • Learning Goals:
    • Learn how to further generalize the functionality of a cake by introducing input parameters for every possible variable attribute of the block function.
    • Gain some further experience with the concept of abstraction as a big idea in Information science.
  • Tips:
    • It may be a good idea to highlight that in this page students will be further generalizing the pinwheel block by by introducing more input parameters. Again, this is an example of brainchild.
    • Some students may take difficulty creating the size parameter in betwixt the branches and the fill-in parameters. It may help to point them to the "+" sign in between these two parameters.
    • On the If There Is Time circle problem, some students may demand assistance realizing that a regular polygon with a big number of sides, for example a thirty-gon, is a expert approximation for a circumvolve.
• Page 5: Using Pinwheel to Make Polygon.
  • Learning Goals:
    • Learn how to tailor a general-purpose procedure to create other, simpler special-purpose procedures that each practise a particular job.
    • Understand how to depict polygons in Snap!.
  • Tips:
    • On the If There Is Fourth dimension circle cake-building problem, the students may need help discovering what should the one input exist for a circumvolve block. A natural choice for the unmarried input would exist "radius". The students may demand a reminder from the previous folio that a regular polygon with a large number of sides, for example a 30-gon, is a expert approximation for a circumvolve. The difficulty in this instance volition be determining the "side length" of the approximating polygon. Students can find this past experimenting or it may be helpful to remind them that for a regular polygon:
      \text{side length} = \frac{\text{perimeter}}{\text{number of sides}} \approx \frac{two \pi \cdot \text{radius}} {\text{number of sides}}
• Page half-dozen: Looping with a Counter.
  • Learning Goals:
    • Learn the similarities and differences between the forever, repeat, and for blocks.
    • Empathize the power of a loop counter.
  • Tips:
    • Highlight that the for block, in addition to providing looping functionality like to the forever and echo blocks, also provides access to the individual stages of a loop with the use of a counter; this enhances the possibilities of what tin be accomplished by looping.
    • Most students may not realize that it is possible to loop backwards with the for block past letting the index showtime from a larger number and finish with a smaller number as shown at correct. This code will have the sprite count backwards from 10 to 1.
• Folio vii: Keeping a Programming Journal.
  • Learning Goals:
    • Sympathise the purpose and contents of a programming journal.
  • Tips:
    • Review the "Journals" section of the Introduction to Instructor Guide.

Solutions

Correlation with 2020 AP CS Principles Framework

Computational Thinking Practices: Skills

• 2.A: Represent algorithmic processes without using a programming linguistic communication.
• 3.B: Apply abstraction to manage complexity in a program.
• 4.A: Explicate how a code segment or program functions.
• iv.B: Determine the result of lawmaking segments.

Learning Objectives:

• CRD-2.Thou: Draw the purpose of a code segment or program past writing documentation. (four.A)
• AAP-2.A: Express an algorithm that uses sequencing without using a programming language. (two.A)
• AAP-iii.A: For procedure calls:
  1. Write statements to call procedures. (3.B)
  2. Determine the result or effect of a procedure call. (iv.B)

Essential Noesis:

• CRD-2.B.3: A program needs to work for a diversity of inputs and situations.
• CRD-2.G.1: Program documentation is a written description of the office of a code segment, event, procedure, or program and how it was adult.
• CRD-2.Grand.ii: Comments are a form of programme documentation written into the programme to be read by people and do not affect how a plan runs.
• CRD-2.G.iii: Programmers should certificate a program throughout its evolution.
• CRD-2.Yard.iv: Plan documentation helps in developing and maintaining right programs when working individually or in collaborative programming environments.
• CRD-two.G.v: Non all programming environments support comments, and then other methods of documentation may exist required.
• DAT-ane.A.1: Data values tin be stored in variables, lists of items, or standalone constants and tin can be passed every bit input to (or output from) procedures.
• AAP-two.A.1: An algorithm is a finite set up of instructions that accomplish a specific task.
• AAP-2.A.ii: Across visual and textual programming languages, algorithms can be expressed in a variety of ways, such every bit natural language, diagrams, and pseudocode.
• AAP-ii.A.3: Algorithms executed by programs are implemented using programming languages.
• AAP-two.J.1: Iteration is a repeating portion of an algorithm. Iteration repeats a specified number of times or until a given status is met.
• AAP-two.K.1: Iteration statements change the sequential menses of control by repeating a fix of statements zero or more than times, until a stopping condition is met.
• AAP-2.Yard.two: The exam reference sail provides

  REPEAT n TIMES {     <block of statements> }

  in which the

  cake of statements

  is executed

  due north

  times.
• AAP-3.A.three: Parameters are input variables of a procedure. Arguments specify the values of the parameters when a procedure is called.
• AAP-three.A.4: A process call interrupts the sequential execution of statements, causing the plan to execute the statements within the procedure before continuing. Once the last argument in the procedure (or a render statement) has executed, menstruation of command is returned to the betoken immediately following where the procedure was called.
• AAP-iii.A.v: The test reference sail provides

  procName (arg1, arg2, …)

  equally a style to call

  PROCEDURE procName(parameter1, parameter 2, …)

  which takes zero or more arguments;

  arg1

  is assigned to

  parameter1

  ,

  arg2

  is assigned to

  parameter2

  , and so on.
• AAP-3.B.4: A procedural abstraction may extract shared features to generalize functionality instead of duplicating code. This allows for program code reuse, which helps manage complexity.
• AAP-3.B.v: Using parameters allows procedures to be generalized, enabling the procedures to be reused with a range of input values or arguments.
• AAP-iii.B.7: Using procedural abstraction in a programme allows programmers to change the internals of the procedure (to brand information technology faster, more efficient, apply less storage, etc.) without needing to notify users of the change as long as what the procedure does is preserved.
• AAP-three.C.1: The exam reference sheet provides

  PROCEDURE procName(parameter1, parameter2, …) {     <block of statements> }

  which is used to define a process that takes zero or more arguments. The procedure contains

  cake of statements

  .

Can nosotros delete these "old mathematical notes"? --MF, 11/4/19

Old Mathematical Notes:

• Mathematics Annotation: Direction. Snap! reports the direction that a sprite is facing using a system similar to that used by a magnetic compass:
  • 0 is direct up, facing the top of the screen
  • 90 faces the right-hand side of the screen
  • 180 points "due s"
  • 270 faces the left-hand side of the screen
  The inputs to the point in direction block tin be any number, and this gives an opportunity to talk about different inputs to point in direction that produce the same effect. Try, for example, turning on the direction reporter in the Motion palette (it reports the direction of the sprite), but endeavour using indicate in direction with an input of -20 and then once more with an input of 340. The sprite points the same way—nothing changes—merely direction reports -20 and and so 340. Conspicuously, -20 ≠ 340, simply they differ past 360: 340 = -twenty + 360 Sprite direction is adamant only up to multiples of 360, because a complete turn is 360° and that brings you back to where you lot started. So, using inputs to point in direction that are multiples of 360: 0,360,720,1080,... will all bring you dorsum to pointing directly up, and similarly, inputs that are, say, 75 more than these: 75,75+360,75+720,75+1080,... will all do the same thing every bit point in direction with an input of 75. The mathematical autograph for this is to say something like "75 is the same equally 435 modulo 360, which tin can exist expressed in Snap! as shown at right. (The discussion modulo was introduced by Gauss equally a way to say "except for multiples of." These days, the meaning is often used in other ways, like "The game volition have place today, modulo rain.")
• Mathematics Note: Circles. Yous sometimes hear people say "a circle is a polygon with an infinite number of sides." This isn't true in any precise sense, simply it is true that a circle can be approximated by a polygon with many sides, each very short in length. This is similar to what children practice when the walk effectually a circumvolve—they take many small steps. And this is how Snap! models circles—it creates a polygon with many small turns and steps. For case:
  
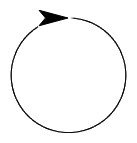
  This looks very much similar a circle, only it'south really a polygon with 360 sides, all of length 1 pace.
  In particular, y'all tin can apply facts about circles to these Snap! approximations, and they work quite well. For example, in the Have it Further challenge, the diameter of the reddish circumvolve is 100. The circumference (perimeter) of a circumvolve is π times its diameter. If your students know this fact, then they tin reason that the circumference of the carmine circle is 100π. Using the approximation 3.14 for π, the circumference is approximately 314. So, if we want to encompass this distance in 360 steps, the step size should be \frac{314}{360}. Snap! tin can practice the calculation for us.
  

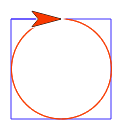
hodgedooketherver.blogspot.com

Source: https://bjc.edc.org/bjc-r/cur/teaching-guide/U1/lab-pages/3-modern-art-polygons.html?topic=nyc_bjc%2F1-teaching-guide.topic&course=bjc4nyc_teacher.html&novideo&noassignment

Share this post